#<- misread “5679 fishing rods used” as having fully used up 5679 fishing rods

[locusfandomtime]

Doing the maths: Grian's failure at getting a mending book

lots of talk about maths and probabilities below the cut! but there's a graph and simple explanation at the end if you want to get the gist of it and are bad at maths.

(I am still young and learning maths, critique/advice always welcomed)

What are the odds of getting a mending book in Minecraft?

(I am assuming Grian has been doing all his fishing with Luck of the Sea 3)

The probability of a mending book is actually a bit annoying to estimate. The Minecraft Wiki lists fishing up an enchanted book as 1.9% chance. This is for ANY enchanted book. The Minecraft wiki talks about how the chance of an enchantment being selected is calculated. Mending has a weight of 2. Using the table, mending has a probability of 2/135.

However, Grian is looking for any book with mending, not just a pure mending book. Additional enchantments are calculated in a different way, involving RNG, which means it won't be as easy to model. Due to this reason, I'll just be using the odds for a pure mending book throughout.

TLDR: a mending book has a 0.028..% chance (2/135*0.019*100)

Grian's Data

According to this screenshot, Grian has used a fishing rod 5679 times. This number may not be fully accurate, as it includes the times he's fished other players, rather than just fished for items, but it is a good estimate.

To help visualise this data, with a median waiting time between catches of 17.5 seconds, Grian has spent over 20 hours fishing so far! He may have a problem.

Is this statistically significant?

Hypothesis testing (p-value approach):

H0: p = 19/67500 (the null hypothesis - he has no mending books because of chance)

H1: p < 19/67500 (the alternate hypothesis - he has no mending books due to different odds)

5679 trials, 0 mending books

X ~ B(5679, 19/67500) (binomial distribution, 5679 tries with a probability of a mending book being 19/67500, where X is the number of mending books)

p(X=0) (what is the probability the number of mending books being 0)

p = 0.2021473392

Now, the point at which data becomes significant is subjective. For instance, you *could* get a million heads in a row flipping a coin, it's not impossible, but at a certain point, you can begin to say "okay there's something not normal about this". For this approach, the closer the p-value is to 0, the more evidence there is against the null hypothesis . The p-value here is far above a significance level of 0.01, or 0.05, or 0.1. There isn't a clear line between significant/non-significant, but this is answer is quite a bit far from 0

With this, I cannot reject the null hypothesis.

Personal conclusion: this is not statistically significant, Grian is just unlucky.

Are other values statistically significant?

Gem's proposed 9000: results in a p-value of 0.079... more significant than Grian's number but I don't imagine Mojang would be too concerned. As said though, it's all subjective.

I am bad at maths, what does all this mean?

Here is a graph, showing what number of mending books you might have after 5679 tries. The height of the bar represents the probability of getting that amount. The numbers at the top are the (rounded) numbers I used in my calculation

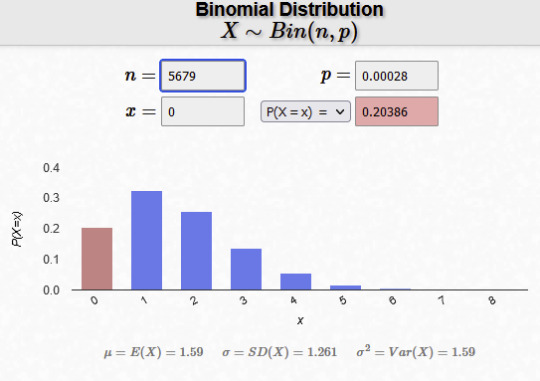
The pink column is 0 mending books - like what Grian has! As you can see, it is less likely than getting 1 or 2 books, but not too uncommon to happen.

End conclusion: Grian has bad luck. Like, not as hilariously bad as he thinks, but still bad. If he keeps going, chances are he will get a mending book, but I think he should probably stop fishing because at this point he has a problem.